TURN BACK AFTER AN ENGINE FAILURE?
If you ever want to get a bunch of pilots to start a heated discussion, just throw out the question:
When is it safe to turn back to the airport after an engine failure during climb-out?
The discussion will usually center on altitude; 800 feet above ground, 1000 feet, or 1500 feet?
Surprisingly, many pilots will agree that once you reach an altitude of 1000 feet, a return back to the runway you just departed from is possible after an engine failure. In aviation text books, the recommended action when experiencing engine failure during climb-out is to lower the nose and land straight ahead, with small course changes left or right to avoid the worst kind of obstacles.
Before proceeding further, a note of warning:
The following discussion, calculations and results are not to be used for any decision to attempt a turn back to the airport following an engine failure after take-off. This page is meant to encourage discussion and reflection on the action taken. The equations address highly idealized situations and do not reflect the real world.
The point I will argue here is that it is simply impossible to return to the point of take-off, and that the question itself is wrong. The reason for this is easy to see if one calculates the angle of best climb rate, that is, the angle between the ground and the flight path achieved when climbing at best rate of climb (Vy), which is essentially identical to the angle between the flight path and the ground when descending on the best glide speed. This is valid, with small variations, for most single engine propeller aircraft. If these two angles are identical, in order to get back to your point of departure you need to turn the airplane around 180 degrees without loosing any altitude at all. Clearly an impossible feat. This observation does not depend on altitude. It doesn't matter whether the engine quits at 1000 feet AGL, 2000 feet or even 10,000 feet, you will not make it back to the POD (Point of Departure). This is illustrated in the figure below.
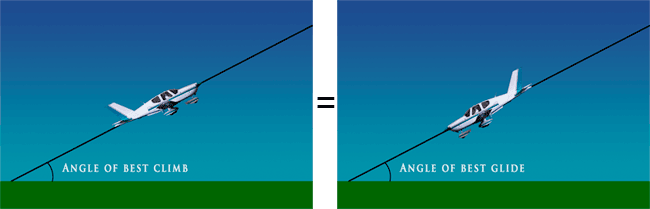
Although the "secret" with the turn back to the airport scenario is to be found in the angles of best rate of climb (Vy) and angle resulting from the best glide speed, these angles are not given in the POH. However, they can easily be calculated with a bit of trigonometry.
A bit of trigonometry
Here is a simple calculation of the angles involved. In the derivation we need to specify the speed for best rate of climb (Vy), the climb rate associated with that speed (vfpm) and the glide ratio (R). All these values can be found on the POH or equivalent document. The factor 101.24 is to transform feet-per-minute to knots, the same unit as Vy. The angles are then simply the inverse sinus and inverse tangent, respectively. Any decent handheld calculator can handle that calculation.
If we plug in some values for a Cessna Skyhawk S-model, we find Vy = 74 knots, Vfpm = 710 fpm and the glide ratio is 9.1. These values are for full weight and at sea level, if these circumstances change, the appropriate values need to be adjusted. Plugging this into the equations give us an angle for best rate of climb of 5.4 degrees, and an angle for best glide of 6.3 degrees. Here the situation is pretty bad: the angle for best glide is larger than for Vy, meaning that in order to make it back to the point of departure (POD), you have to gain altitude in the turn – without an engine producing power this is something very difficult (to say the least). In this case the situation just gets worse as altitude increases!
For a C182T the corresponding values are: Vy = 80 knots, Vfpm = 905 fpm and the glide ratio R = 8.7. Plugging in these values we get a angle for best rate of climb of 6.4 degrees, and an angle for best glide of 6.6 degrees. Almost identical and again with the implied result that a turn back to the POD is impossible regardless of altitude!
The real issues (and some more trigonometry)
The problem with the above analysis is that unless one is departing the Juancho E. Yrausquin Airport on Saba (an island in the Caribbean with a runway 
length of 1312 feet – the world's shortest runway with commercial operations) there is always 'runway remaining' after lift-off. There is also the issue of head-wind component, which increases the effective angle for best climb rate and decreases the angle for best glide. Both actions helping the hapless pilot trying the impossible.
- Runway remaining: in order to return to the airport the pilot don't need to reach the POD (Point of Departure). It is enough to reach the runway. Hence if one is departing a long runway, the effective angle for best glide could be larger than the one calculated above.
- Head-wind component: Any head-wind component will make the distance needed to return to the airport shorter than in a no-wind condition.
The question we will ask is: How much altitude can a pilot loose in the turn that will point the airplane back towards the airport and still make it back to the threshold? The assumptions made here are: (1) the turn is completed at a point which is as far away from the intended touch down point as the airplane was when the engine failed (there's a hand-drawn figure illustrating this below), (2) in the case of a head-wind component, it is constant with altitude all through the calculations.
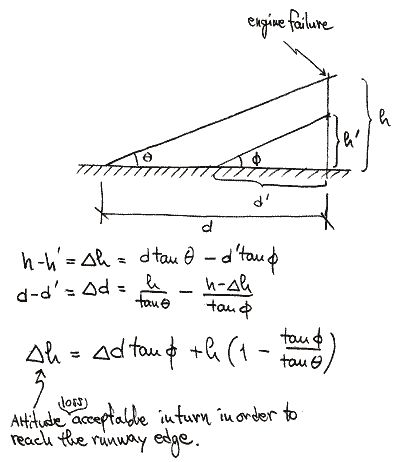Runway Remaining
First lets look at the runway remaining issue (maintaining a no-wind assumption). The figure to the left illustrates the situation where h is the altitude reached when the engine fails, and h' is the altitude when the airplane is pointing towards the runway and at the same distance as when the engine failed. The distance d' is the distance needed in order to return to the runway threshold. Using the values for C172S derived above, and assuming we had 2000' of runway remaining when we lifted off (for a Skyhawk this would correspond to a 3000' long runway), and furthermore assume that the engine fails at an altitude of 1000', the 'acceptable' altitude loss in the turn back to the airport is 53 feet! Again, the implication is LAND STRAIGHT AHEAD. If we increase the altitude of engine failure to 3000', the pilot will need to gain 283' in the turn. This is due to the fact that the glide angle is larger (i.e. steeper) than the climb angle in this case. For the Skylane (T model), the corresponding value, for an engine failure at 1000', is 200'. That is, the pilot is allowed to loose 200' in the turn back to the airport and still make the runway threshold. Increasing the altitude to 3000' and the acceptable altitude loss in the turn becomes 160'. If the remaining runway length is longer, the acceptable altitude loss increases a bit – but not by a whole lot. Feel free to do the calculations yourself.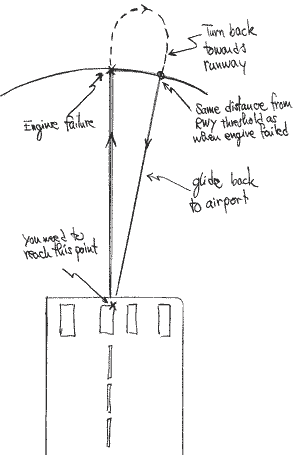
Head-wind Component
Adding a wind correction makes it a bit more complicated, but the calculations are still manageable if we assume that the headwind component is constant and independent on altitude. We need to introduce the best glide speed (Vgs) in the calculations. Apart from this, the trick is to define 'effective' climb and glide angles and then use these in the equation for acceptable altitude loss (see above). Again we assume that the altitude loss is done during the turn back towards the airport and when the airplane is at the same distance from the threshold as when the engine failed we can start a normal glide (and the head-wind component has magically remained the same). Note that the calculations do not concern itself with the turn (how steep, which direction, wind effects, etc). The calculations simply assess how much altitude that is allowed during the turn in order for the pilot to make it back to the runway threshold. If you would be further away from the runway that when the engine failed, the calculations are not valid. The situation is depicted in the figure to the right.
Ok, back to the wind corrections. Below are the formulae for applying this. The new parameters are the best glide speed (Vgs) and the head-wind component (w). Apart from this, it is essentially the same as before. Plugging in the numbers for the Skyhawk and the Skylane (assuming a best glide speed of 68 knots for the C172 and 75 knots for the C182), it is clear that the head-wind 
component increase the effective angle of best rate of climb and decrease the angle for best glide. In the tables are the acceptable altitude loss in the turn (delta_h) for head-wind components 0, 10 and 20 knots for an engine failure occurring at 1000 and 3000 feet above airport elevation. The remaining runway is set to 2000 feet in both cases.
w (knots) |
delta_h (feet) |
h (feet) |
|---|---|---|
0 |
53 |
1000 |
10 |
284 |
1000 |
20 |
418 |
1000 |
0 |
-283 |
3000 |
10 |
467 |
3000 |
20 |
906 |
3000 |
w (knots) |
delta_h (feet) |
h (feet) |
|---|---|---|
0 |
207 |
1000 |
10 |
391 |
1000 |
20 |
510 |
1000 |
0 |
160 |
3000 |
10 |
767 |
3000 |
20 |
1166 |
3000 |
The bottom line
The discussion of this scenario tends to focus on which altitude one can safely return to the airport. What I wanted to show here is that this is misleading and that the important issues are (1) runway remaining at the point of take-off, and (2) the head-wind component during climb-out. However, even when taking these factors into consideration, it is basically impossible to return to the airport. The bottom line of all this is that a turn back to the runway after an engine failure is not recommended, regardless of altitude. Before the pilot reacts to the sudden loss of engine power, gets the nose down enough to regain gliding speed and then starts the turn, so much altitude is lost that it is better to find an alternate landing site straight ahead – and in some case the pilot needs to gain altitude in the turn in order to make it back.
Another important point to make from this discourse is that my handwriting needs some serious improvement. Most people (including myself) have a hard time interpeting my scribbles...
Finally
an additional note of warning: The calculations presented here are not accurate and should not be the basis of any in-flight decision of attempting a return to the airport following an engine failure. They are meant to illustrate the difficulty and the likelihood of a negative outcome of such an attempt.